




Next: Example (from Program LA_GBSVX_EXAMPLE)
Up: General Linear Systems
Previous: Description
Contents
Index
- AB
- (input/output) REAL or COMPLEX
rectangular array, shape
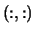 with
with
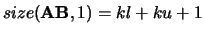 and
and
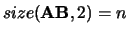 , where
, where  and
and  are, respectively, the numbers of subdiagonals and
superdiagonals in the band of
are, respectively, the numbers of subdiagonals and
superdiagonals in the band of 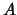 , and
, and  is the order of
is the order of 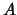 .
.
On entry, the matrix 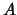 or its equilibration in
band storage. The
or its equilibration in
band storage. The  diagonals of
diagonals of 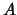 are stored
in rows
are stored
in rows 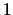 to
to  of AB,
so that the
of AB,
so that the 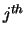 column of
column of 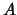 is stored in the
is stored in the 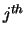 column of AB as follows:
column of AB as follows:
The remaining elements in  need not be set.
need not be set.
If 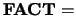 'F' and
'F' and
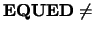 'N' then
'N' then 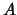 has been equilibrated by the scaling factors in
has been equilibrated by the scaling factors in 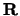 and/or
and/or 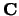 during the previous call to LA_GBSVX.
during the previous call to LA_GBSVX.
On exit, if 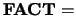 'E',
the equilibrated version of
'E',
the equilibrated version of 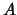 is stored in AB; otherwise,
is stored in AB; otherwise,
 is unchanged.
is unchanged.
- B
- (input/output) REAL or COMPLEX array, shape
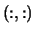 with
with
 or shape
or shape  with
with
 .
.
On entry, the matrix 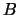 .
.
On exit, the scaled version of 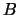 if the system has been equilibrated;
otherwise,
if the system has been equilibrated;
otherwise,  is unchanged.
is unchanged.
- X
- (output) REAL or COMPLEX array, shape
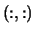 with
with
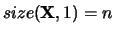 and
and
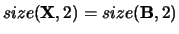 ,
or shape
,
or shape  with
with
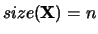 .
.
The solution matrix  .
.
- KL
- Optional (input) INTEGER.
The number of subdiagonals in the band of 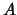 (
( ).
).
The number of superdiagonals in the band is given by
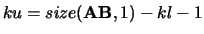 .
.
Default value:
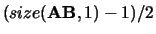 .
.
- AFB
- Optional (input or output) REAL or
COMPLEX rectangular array, shape
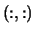 with
with
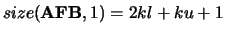 and
and
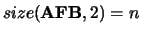
If 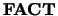 = 'F' then AFB is an input argument
that contains the details of the factorization of (the equilibrated)
= 'F' then AFB is an input argument
that contains the details of the factorization of (the equilibrated) 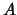 returned by a previous call to LA_GBSVX.
returned by a previous call to LA_GBSVX.
If
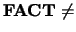 'F' then
'F' then 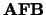 is an output argument
that contains the details of the factorization of (the equilibrated)
is an output argument
that contains the details of the factorization of (the equilibrated) 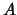 .
.
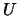 is an upper triangular band matrix
with
is an upper triangular band matrix
with  diagonals. These are stored in the
first
diagonals. These are stored in the
first  rows of
rows of 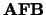 . The multipliers that
arise during the factorization are stored in the remaining rows.
. The multipliers that
arise during the factorization are stored in the remaining rows.
- IPIV
- Optional (input or output) INTEGER array, shape
 with
with
 .
.
If 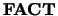 = 'F' then
= 'F' then  is an input
argument that contains the pivot indices from the factorization
of (the equilibrated)
is an input
argument that contains the pivot indices from the factorization
of (the equilibrated) 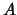 , returned by a previous call to LA_GBSVX.
, returned by a previous call to LA_GBSVX.
If
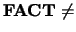 'F' then
'F' then  is an output
argument that contains the pivot indices from the factorization
of (the equilibrated)
is an output
argument that contains the pivot indices from the factorization
of (the equilibrated) 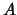 .
.
- FACT
- Optional (input) CHARACTER(LEN=1).
Specifies whether the factored form of the matrix 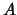 is
supplied on entry, and, if not, whether the matrix
is
supplied on entry, and, if not, whether the matrix 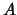 should be
equilibrated before it is factored.
should be
equilibrated before it is factored.
![\begin{optionarg}
\item[{= 'N':}] The matrix $A$\ will be copied to {\bf AFB} a...
...{\bf IPIV} contain the
factored form of (the equilibrated) $A$.
\end{optionarg}](img328.gif)
Default value: 'N'.
- TRANS
- Optional (input) CHARACTER(LEN=1).
Specifies the form of the system of equations:
![\begin{optionarg}
\item[{= 'N':}] $AX=B$\ (No transpose)
\item[{= 'T':}] $A^TX=B$\ (Transpose)
\item[{= 'C':}] $A^HX=B$\ (Conjugate transpose)
\end{optionarg}](img256.gif)
Default value: 'N'.
- EQUED
- Optional (input or output) CHARACTER(LEN=1).
Specifies the form of equilibration that was done.
 is an input argument if
is an input argument if 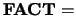 'F', otherwise it
is an output argument:
'F', otherwise it
is an output argument:
![\begin{optionarg}
\item[{= 'N':}] No equilibration (always true if {\bf FACT} =...
...({\bf C})$.
\item[{= 'B':}] Both row and column equilibration.
\end{optionarg}](img258.gif)
Default value: 'N'.
- R
- Optional (input or output) REAL array, shape
 with
with
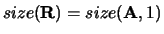 .
.
The row scale factors for 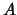 .
.
R is an input argument if FACT = 'F' and
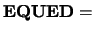 'R' or 'B'.
'R' or 'B'.
R is an output argument if FACT = 'E' and
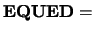 'R' or 'B'.
'R' or 'B'.
- C
- Optional (input or output) REAL array, shape
 with
with
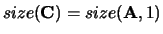 .
.
The column scale factors for 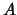 .
.
C is an input argument if FACT = 'F' and 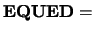 'C' or 'B'.
'C' or 'B'.
C is an output argument if FACT = 'E' and
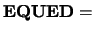 'C' or 'B'.
'C' or 'B'.
- FERR
- Optional (output) REAL array
of shape
 , with
, with
 , or REAL scalar.
, or REAL scalar.
The estimated forward error bound for each solution vector
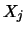 (the
(the  -th column of the solution matrix
-th column of the solution matrix  ).
If
).
If 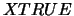 is the true solution corresponding to
is the true solution corresponding to 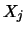 ,
, 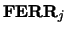 is an estimated upper bound for the magnitude of the largest
element in
is an estimated upper bound for the magnitude of the largest
element in 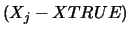 divided by the magnitude of the
largest element in
divided by the magnitude of the
largest element in 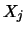 . The estimate is as reliable as
the estimate for RCOND and is almost always a slight
overestimate of the true error.
. The estimate is as reliable as
the estimate for RCOND and is almost always a slight
overestimate of the true error.
- BERR
- Optional (output) REAL array
of shape
 , with
, with
 , or REAL scalar.
, or REAL scalar.
The componentwise relative backward error of each solution
vector 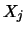 (i.e., the smallest relative change in
any element of
(i.e., the smallest relative change in
any element of 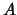 or
or 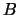 that makes
that makes 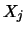 an exact solution).
an exact solution).
- RCOND
- Optional (output) REAL.
The estimate of the reciprocal condition number of (the equilibrated)
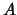 . If RCOND is less than the machine precision, the matrix
is singular to working precision. This condition is indicated by
a return code of INFO
. If RCOND is less than the machine precision, the matrix
is singular to working precision. This condition is indicated by
a return code of INFO 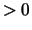 .
.
- RPVGRW
- Optional (output) REAL.
The reciprocal pivot growth
factor
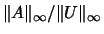 .
If RPVGRW is much less than
.
If RPVGRW is much less than 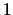 , then the stability
of the
, then the stability
of the 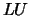 factorization of the (equilibrated) matrix
factorization of the (equilibrated) matrix 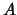 could be poor. This also means that the solution
could be poor. This also means that the solution  , condition
estimator RCOND, and forward error bound
, condition
estimator RCOND, and forward error bound 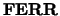 could be
unreliable. If the factorization fails with
could be
unreliable. If the factorization fails with
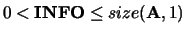 ,
then RPVGRW contains the reciprocal pivot growth factor for
the leading INFO columns of
,
then RPVGRW contains the reciprocal pivot growth factor for
the leading INFO columns of 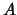 .
.
- INFO
- Optional (output) INTEGER
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if ${\bf IN...
...urate than the
value of {\bf RCOND} would suggest.
\end{infoarg} \end{infoarg}](img272.gif)
If  is not present and an error occurs, then the program
is terminated with an error message.
is not present and an error occurs, then the program
is terminated with an error message.
References: [1] and [17,9,20,21].





Next: Example (from Program LA_GBSVX_EXAMPLE)
Up: General Linear Systems
Previous: Description
Contents
Index
Susan Blackford
2001-08-19
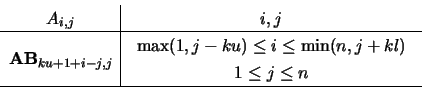
![\begin{optionarg}
\item[{= 'N':}] The matrix $A$\ will be copied to {\bf AFB} a...
...{\bf IPIV} contain the
factored form of (the equilibrated) $A$.
\end{optionarg}](img328.gif)
![\begin{optionarg}
\item[{= 'N':}] $AX=B$\ (No transpose)
\item[{= 'T':}] $A^TX=B$\ (Transpose)
\item[{= 'C':}] $A^HX=B$\ (Conjugate transpose)
\end{optionarg}](img256.gif)
![\begin{optionarg}
\item[{= 'N':}] No equilibration (always true if {\bf FACT} =...
...({\bf C})$.
\item[{= 'B':}] Both row and column equilibration.
\end{optionarg}](img258.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if ${\bf IN...
...urate than the
value of {\bf RCOND} would suggest.
\end{infoarg} \end{infoarg}](img272.gif)