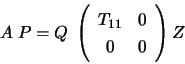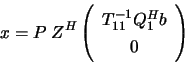Next: Arguments
Up: Linear Least Squares Problems
Previous: LA_GELSY
Contents
Index
LA_GELSY computes the minimum-norm least squares solution to one or
more real or complex linear systems  using a complete orthogonal
factorization of
using a complete orthogonal
factorization of 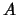 . Matrix
. Matrix 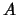 is rectangular and may be rank-deficient.
The vectors
is rectangular and may be rank-deficient.
The vectors 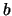 and corresponding solution vectors
and corresponding solution vectors 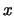 are
the columns of matrices denoted
are
the columns of matrices denoted 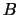 and
and  , respectively.
, respectively.
The routine computes a 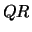 factorization of
factorization of 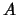 with column pivoting:
with column pivoting:
where  is the largest leading submatrix whose estimated
condition number is less than
is the largest leading submatrix whose estimated
condition number is less than 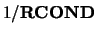 . The order of
. The order of  ,
,
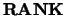 , is the effective rank of
, is the effective rank of 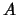 .
.
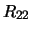 is considered to be negligible, and
is considered to be negligible, and 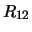 is annihilated
by orthogonal (unitary) transformations from the right, yielding the
complete orthogonal (unitary) factorization
is annihilated
by orthogonal (unitary) transformations from the right, yielding the
complete orthogonal (unitary) factorization
The minimum-norm least squares solution is then
where 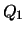 consists of the first
consists of the first 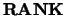 columns of
columns of 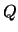 .
.





Next: Arguments
Up: Linear Least Squares Problems
Previous: LA_GELSY
Contents
Index
Susan Blackford
2001-08-19
![]() using a complete orthogonal
factorization of
using a complete orthogonal
factorization of ![]() . Matrix
. Matrix ![]() is rectangular and may be rank-deficient.
The vectors
is rectangular and may be rank-deficient.
The vectors ![]() and corresponding solution vectors
and corresponding solution vectors ![]() are
the columns of matrices denoted
are
the columns of matrices denoted ![]() and
and ![]() , respectively.
, respectively.
![]() factorization of
factorization of ![]() with column pivoting:
with column pivoting: